首发于CSDN

KMP算法

next数组构建

定义： 对于字符串p，next[i]表示p在[0, i]上的子串的最长相同前后缀长度

暴力求解： 很明显，可以在[0, i)上枚举长度来构建next，此时算法复杂度为O(m^2)，m为p的长度

优化求解： 见到最长两字容易想到使用递推也就是动态规划去求解，此时状态就是next数组的定义；求解next[i]时已知字串[0, i-1]的最长相同前后缀长度next[i-1]=j，也就是说该子串对应前缀为子串[0, j)；此时出现两种情况：

1. p[j] = p[i]，有next[i] = next[i-1]+1；

2. p[j] != p[i]，此时需要 不断缩短子串[0, j)，找到子串[0, i)上的次长相同前后缀长度， 但我们只知道最长相同前后缀长度next[i-1]；但不难由next[i-1] = j得子串[0, j)等于子串[i-j, i)，而子串[0, i)的次长相同前后缀的前缀必定落在子串[0, j)上、后缀必定落在子串[i-j, i)上，设子串[0, i-1]的次长相同前后缀为[0, k)和[i-k, i)， 则有子串[k, j)==[i-k, i)==[0, k)，求解子串[0, i)次长相同前后缀问题可转化为求解子串[0, j)的最长相同前后缀，也就是next[j-1]； 不断递归j = next[j-1]直至p[j] == p[i]或j == 0，要么没找到相同字符，此时next[i] = 0，要么找到了，此时next[i] =s j+1； 此时根据均摊分析可知复杂度为O(m)

字符串匹配

首先想到的还是暴力求解：每次匹配失败时指针i在主串S上回到初始位置并向后移动一格，指针j在模式串P上回到初始位置

由上图可知这种移动方式是非常耗时的，因为字符c在前面几个字符ab中并没有出现，完全可以直接将模式串P相对于主串S移动到指针i指向的字符a处。

优化求解： 对于指针j，next[j-1]表示子串[0, j-1]的最长相同前后缀；

如果next[j-1] = 0，意味着 字符P[j-1]不会出现在P[0, j-2]上，而且因为P和S已部分匹配， 有S[i-j, i-1] = P[0, j-1]，因此有$\forall k \in [0, j-2], P[k] \neq S[i-1]$，即模式串P相对于主串 S移动[1, j-2]位， 都不会把S[i-1]匹配上， 这时候就可以把S[i-1]放弃掉，此时对应的就是上面那种情况。

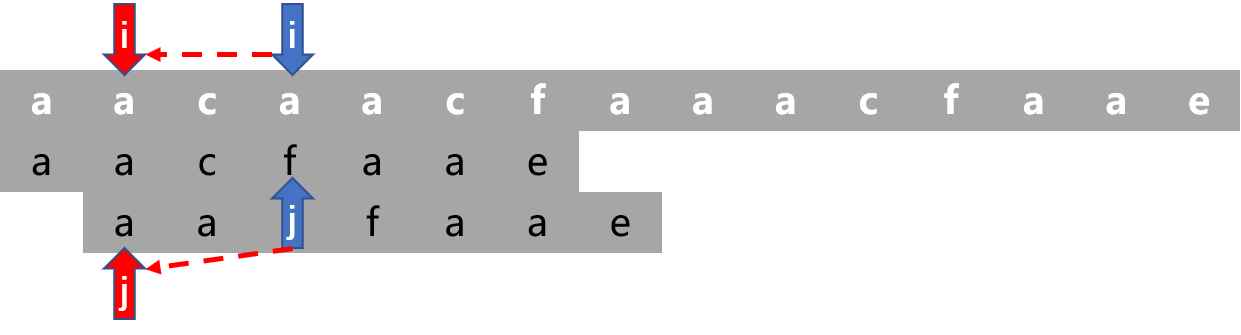
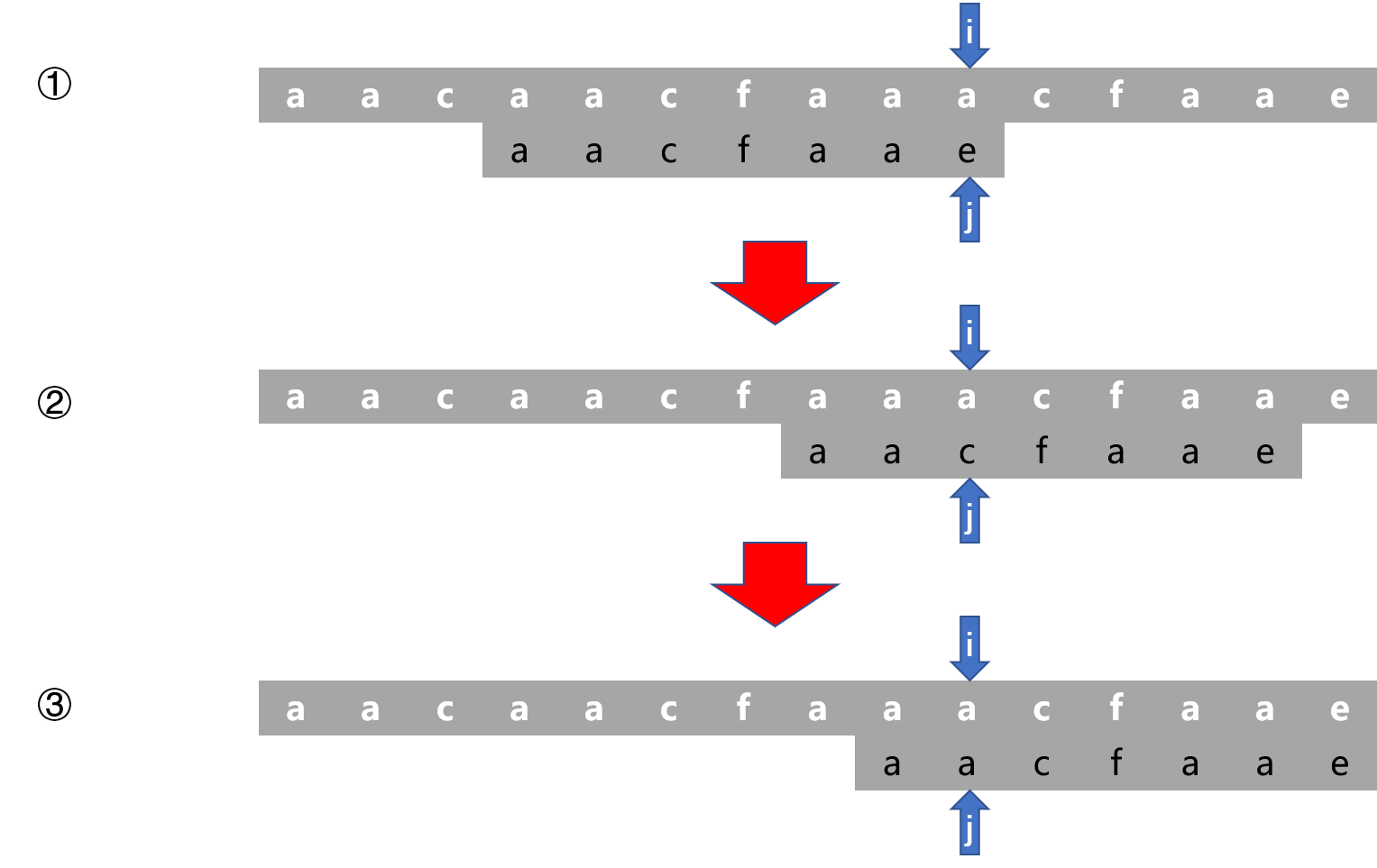
对于一般的next[j-1] != 0，如下图，此时next[j-1] = 2，同样的也有S[i-j, i-1] = P[0, j-1]，因此有 P[j-2, j-1] = S[i-2, i-1] = P[0, 1]， 也就是说 P[0]和P[1]是能够匹配上S[i-2]和S[i-1]的， 可以将P相对于S移动到该位置继续匹配S[i]和P[j]，如下图①和②；

但此时S[i]和P[j]依旧没有匹配上，且有next[j-1] = 1，继续移动，如上图②和③，S[i]和P[j]终于匹配上了，且随着i和j同时继续往下走，模式串P终于匹配上主串S；

这个过程中存在一个递归关系j = next[j-1]，且递归终止条件为j==0 || S[i] == P[j] ， 这里的递归公式与动态求解 next数组一致， 这个过程中j越来越小也就是说相对于初始位置、P相对于S移动的量越来越大， 能够排除暴力求解中的一些情况的同时不漏掉所有可能匹配上的情况。

CPP代码

int strStr(string haystack, string needle) {
    int m = needle.size(), n = haystack.size();
    if (m == 0) return 0;
    if (n < m) return -1; 
    vector<int> next(m);
    for (int i = 1, j = 0; i < m; ++i) {
        while (j > 0 && needle[i] != needle[j]) j = next[j-1];
        if (needle[i] == needle[j]) ++j;
        next[i] = j;
    }
    for(int i = 0, j = 0; i < n; ++i) {
        while (j>0 && haystack[i] != needle[j]) j = next[j-1];
        if (haystack[i] == needle[j]) {
            ++j;
            if (j == m) return i-m+1;
        }
    }
    return -1;
}
CPP